Many of the challenges that we face in delivering effective and affordable health care do not have well understood and generally accepted solutions.
Many of the challenges that we face in delivering effective and affordable health care do not have well understood and generally accepted solutions.
If they did there would be no discussion or debate about what to do and the results would speak for themselves.
This lack of understanding is leading us to try to solve a complicated system design challenge in our heads. Intuitively.
And trying to do it this way is fraught with frustration and risk because our intuition tricks us. It was this sort of challenge that led Professor Rubik to invent his famous 3D Magic Cube puzzle.
It is difficult enough to learn how to solve the Magic Cube puzzle by trial and error; it is even more difficult to attempt to do it inside our heads! Intuitively.
And we know the Rubik Cube puzzle is solvable, so all we need are some techniques, tools and training to improve our Rubik Cube solving capability. We can all learn how to do it.
Returning to the challenge of safe and affordable health care, and to the specific problem of unscheduled care, A&E targets, delayed transfers of care (DTOC), finance, fragmentation and chronic frustration.
This is a systems engineering challenge so we need some systems engineering techniques, tools and training before attempting it. Not after failing repeatedly.
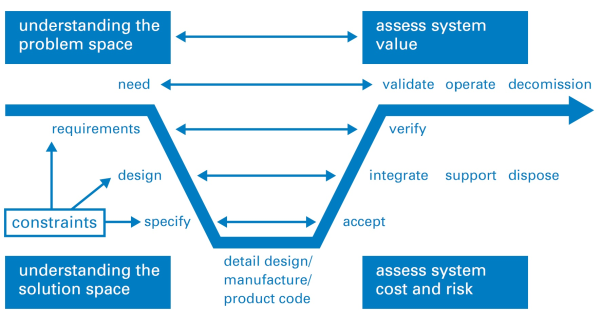
One technique that a systems engineer will use is called a Vee Diagram such as the one shown above. It shows the sequence of steps in the generic problem solving process and it has the same sequence that we use in medicine for solving problems that patients present to us …
Diagnose, Design and Deliver
which is also known as …
Study, Plan, Do.
Notice that there are three words in the diagram that start with the letter V … value, verify and validate. These are probably the three most important words in the vocabulary of a systems engineer.
One tool that a systems engineer always uses is a model of the system under consideration.
Models come in many forms from conceptual to physical and are used in two main ways:
- To assist the understanding of the past (diagnosis)
- To predict the behaviour in the future (prognosis)
And the process of creating a system model, the sequence of steps, is shown in the Vee Diagram. The systems engineer’s objective is a validated model that can be trusted to make good-enough predictions; ones that support making wiser decisions of which design options to implement, and which not to.
So if a systems engineer presented us with a conceptual model that is intended to assist our understanding, then we will require some evidence that all stages of the Vee Diagram process have been completed. Evidence that provides assurance that the model predictions can be trusted. And the scope over which they can be trusted.
Last month a report was published by the Nuffield Trust that is entitled “Understanding patient flow in hospitals” and it asserts that traffic flow on a motorway is a valid conceptual model of patient flow through a hospital. Here is a direct quote from the second paragraph in the Executive Summary:

Unfortunately, no evidence is provided in the report to support the validity of the statement and that omission should ring an alarm bell.
The observation that “the hospitals with the least free space struggle the most” is not a validation of the conceptual model. Validation requires a concrete experiment.
To illustrate why observation is not validation let us consider a scenario where I have a headache and I take a paracetamol and my headache goes away. I now have some evidence that shows a temporal association between what I did (take paracetamol) and what I got (a reduction in head pain).
But this is not a valid experiment because I have not considered the other seven possible combinations of headache before (Y/N), paracetamol (Y/N) and headache after (Y/N).
An association cannot be used to prove causation; not even a temporal association.
When I do not understand the cause, and I am without evidence from a well-designed experiment, then I might be tempted to intuitively jump to the (invalid) conclusion that “headaches are caused by lack of paracetamol!” and if untested this invalid judgement may persist and even become a belief.
Understanding causality requires an approach called counterfactual analysis; otherwise known as “What if?” And we can start that process with a thought experiment using our rhetorical model. But we must remember that we must always validate the outcome with a real experiment. That is how good science works.
A famous thought experiment was conducted by Albert Einstein when he asked the question “If I were sitting on a light beam and moving at the speed of light what would I see?” This question led him to the Theory of Relativity which completely changed the way we now think about space and time. Einstein’s model has been repeatedly validated by careful experiment, and has allowed engineers to design and deliver valuable tools such as the Global Positioning System which uses relativity theory to achieve high positional precision and accuracy.
So let us conduct a thought experiment to explore the ‘faster movement requires more space‘ statement in the case of patient flow in a hospital.
First, we need to define what we mean by the words we are using.
The phrase ‘faster movement’ is ambiguous. Does it mean higher flow (more patients per day being admitted and discharged) or does it mean shorter length of stage (the interval between the admission and discharge events for individual patients)?
The phrase ‘more space’ is also ambiguous. In a hospital that implies physical space i.e. floor-space that may be occupied by corridors, chairs, cubicles, trolleys, and beds. So are we actually referring to flow-space or storage-space?
What we have in this over-simplified statement is the conflation of two concepts: flow-capacity and space-capacity. They are different things. They have different units. And the result of conflating them is meaningless and confusing.
However, our stated goal is to improve understanding so let us consider one combination, and let us be careful to be more precise with our terminology, “higher flow always requires more beds“. Does it? Can we disprove this assertion with an example where higher flow required less beds (i.e. space-capacity)?
The relationship between flow and space-capacity is well understood.
The starting point is Little’s Law which was proven mathematically in 1961 by J.D.C. Little and it states:
Average work in progress = Average lead time X Average flow.
In the hospital context, work in progress is the number of occupied beds, lead time is the length of stay and flow is admissions or discharges per time interval (which must be the same on average over a long period of time).
(NB. Engineers are rather pedantic about units so let us check that this makes sense: the unit of WIP is ‘patients’, the unit of lead time is ‘days’, and the unit of flow is ‘patients per day’ so ‘patients’ = ‘days’ * ‘patients / day’. Correct. Verified. Tick.)
So, is there a situation where flow can increase and WIP can decrease? Yes. When lead time decreases. Little’s Law says that is possible. We have disproved the assertion.
Let us take the other interpretation of higher flow as shorter length of stay: i.e. shorter length of stay always requires more beds. Is this correct? No. If flow remains the same then Little’s Law states that we will require fewer beds. This assertion is disproved as well.
And we need to remember that Little’s Law is proven to be valid for averages, does that shed any light on the source of our confusion? Could the assertion about flow and beds actually be about the variation in flow over time and not about the average flow?
And this is also well understood. The original work on it was done almost exactly 100 years ago by Agner Krarup Erlang and the problem he looked at was the quality of customer service of the early telephone exchanges. Specifically, how likely was the caller to get the “all lines are busy, please try later” response.
What Erlang showed was there there is a mathematical relationship between the number of calls being made (the demand), the probability of a call being connected first time (the service quality) and the number of telephone circuits and switchboard operators available (the service cost).
So it appears that we already have a validated mathematical model that links flow, quality and cost that we might use if we substitute ‘patients’ for ‘calls’, ‘beds’ for ‘telephone circuits’, and ‘being connected’ for ‘being admitted’.
And this topic of patient flow, A&E performance and Erlang queues has been explored already … here.
So a telephone exchange is a more valid model of a hospital than a motorway.
We are now making progress in deepening our understanding.
The use of an invalid, untested, conceptual model is sloppy systems engineering.
So if the engineering is sloppy we would be unwise to fully trust the conclusions.
And I share this feedback in the spirit of black box thinking because I believe that there are some valuable lessons to be learned here – by us all.
To vote for this topic please click here.
To subscribe to the blog newsletter please click here.
To email the author please click here.