January 2013 – HCSE Blog

26/01/2013

Curing Chronic Carveoutosis

Last week the Ray Of Hope briefly illuminated a very common system design disease called carveoutosis. This week the RoH will tarry a little longer to illuminate an example that reveals the value of diagnosing and treating this endemic process ailment.

Do you remember the days when we used to have to visit the Central Post Office in our lunch hour to access a quality-of-life-critical service that only a Central Post Office could provide – like getting a new road tax disc for our car? On walking through the impressive Victorian entrances of these stalwart high street institutions our primary challenge was to decide which queue to join.

In front of each gleaming mahogony, brass and glass counter was a queue of waiting customers. Behind was the Post Office operative. We knew from experience that to be in-and-out before our lunch hour expired required deep understanding of the ways of people and processes – and a savvy selection. Some queues were longer than others. Was that because there was a particularly slow operative behind that counter? Or was it because there was a particularly complex postal problem being processed? Or was it because the customers who had been waiting longer had identified that queue was fast flowing and had defected to it from their more torpid streams? We know that size is not a reliable indicator of speed or quality.

The social pressure is now mounting … we must choose … dithering is a sign of weakness … and swapping queues later is another abhorrent behaviour. So we employ our most trusted heuristic – we join the end of the shortest queue. Sometimes it is a good choice, sometimes not so good! But intuitively it feels like the best option.

Of course if we choose wisely and we succeed in leap-frogging our fellow customers then we can swagger (just a bit) on the way out. And if not we can scowl and mutter oaths at others who (by sheer luck) leap frog us. The Post Office Game is fertile soil for the Aint’ It Awful game which we play when we arrive back at work.

But those days are past and now we are more likely to encounter a single-queue when we are forced by necessity to embark on a midday shopping sortie. As we enter we see the path of the snake thoughtfully marked out with rope barriers or with shelves hopefully stacked with just-what-we-need bargains to stock up on as we drift past. We are processed FIFO (first-in-first-out) which is fairer-for-all and avoids the challenge of the dreaded choice-of-queue. But the single-queue snake brings a new challenge: when we reach the head of the snake we must identify which operative has become available first – and quickly!

Because if we falter then we will incur the shame of the finger-wagging or the flashing red neon arrow that is easily visible to the whole snake; and a painful jab in the ribs from the impatient snaker behind us; and a chorus of tuts from the tail of the snake. So as we frantically scan left and right along the line of bullet-proof glass cells looking for clues of imminent availability we run the risk of developing acute vertigo or a painful repetitive-strain neck injury!

So is the single-queue design better? Do we actually wait less time, the same time or more time? Do we pay a fair price for fair-for-all queue design? The answer is not intuitively obvious because when we are forced to join a lone and long queue it goes against our gut instinct. We feel the urge to push.

The short answer is “Yes”. A single-queue feeding tasks to parallel-servers is actually a better design. And if we ask the Queue Theorists then they will dazzle us with complex equations that prove it is a better design – in theory. But the scary-maths does not help us to understand how it is a better design. Most of us are not able to convert equations into experience; academic rhetoric into pragmatic reality. We need to see it with our own eyes to know it and understand it. Because we know that reality is messier than theory.

And if it is a better design then just how much better is it?

To illustrate the potential advantage of a single-queue design we need to push the competing candiates to their performance limits and then measure the difference. We need a real example and some real data. We are Improvementologists!

First we need to map our Post Office process – and that reveals that we have a single step process – just the counter. That is about as simple as a process gets. Our map also shows that we have a row of counters of which five are manned by fully trained Post Office service operatives.

Now we can measure our process and when we do that we find that we get an average of 30 customers per hour walking in the entrance and and average of 30 cusomers an hour walking out. Flow-out equals flow-in. Activity equals demand. And the average flow is one every 2 minutes. So far so good. We then observe our five operatives and we find that the average time from starting to serve one customer to starting to serve the next is 10 minutes. We know from our IS training that this is the cycle time. Good.

So we do a quick napkin calculation to check and that the numbers make sense: our system of five operatives working in parallel, each with an average cycle time of 10 minutes can collectively process a customer on average every 2 minutes – that is 30 per hour on average. So it appears we have just enough capacity to keep up with the flow of work – we are at the limit of efficiency. Good.

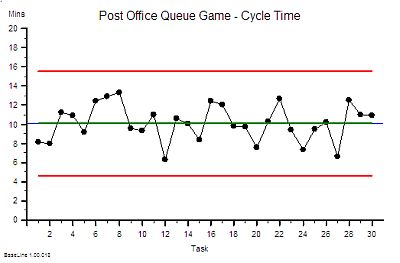We also notice that there is variation in the cycle time from customer to customer – so we plot our individual measurements asa time-series chart. There does not seem to be an obvious pattern – it looks random – and BaseLine says that it is statistically stable. Our chart tells us that a range of 5 to 15 minutes is a reasonable expectation to set.

We also observe that there is always a queue of waiting customers somewhere – and although the queues fluctuate in size and location they are always there.

So there is always a wait for some customers. A variable wait; an unpredictable wait. And that is a concern for us because when the queues are too numerous and too long then we see customers get agitated, look at their watches, shrug their shoulders and leave – taking their custom and our income with them and no doubt telling all their friends of their poor experience. Long queues and long waits are bad for business.

And we do not want zero queues either because if there is no queue and our operatives run out of work then they become under-utilised and our system efficiency and productivity falls. That means we are incurring a cost but not generating an income. No queues and idle resources are bad for business too.

And we do not want a mixture of quick queues and slow queues because that causes complaints and conflict. A high-conflict customer complaint experience is bad for business too!

What we want is a design that creates small and stable queues; ones that are just big enough to keep our operatives busy and our customers not waiting too long.

So which is the better design and how much better is it? Five-queues or a single-queue? Carve-out or no-carve-out?

To find the answer we decide to conduct a week-long series of experiments on our system and use real data to reveal the answer. We choose the time from a customer arriving to the same customer leaving as our measure of quality and performance – and we know that the best we can expect is somewhere between 5 and 15 minutes. We know from our IS training that is called the Lead Time.

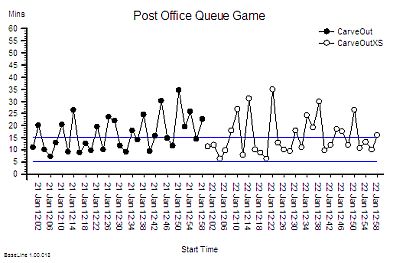
On day #1 we arrange our Post Office with five queues – clearly roped out – one for each manned counter. We know from our mapping and measuring that customers do not arrive in a steady stream and we fear that may confound our experiment so we arrange to admit only one of our loyal and willing customers every 2 minutes. We also advise our loyal and willing customers which queue they must join before they enter to avoid the customer choice challenges. We decide which queue using a random number generator – we toss a dice until we get a number between 1 and 5. We record the time the customer enters on a slip of paper and we ask the customer to give it to the operative and we instruct our service operatives to record the time they completed their work on the same slip and keep it for us to analyse later. We run the experiment for only 1 hour so that we have a sample of 30 slips and then we collect the slips, calculate the difference between the arrival and departure times and plot them on a time-series chart in the order of arrival.

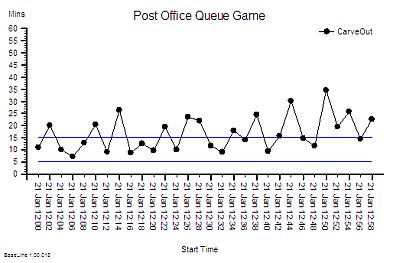This is what we found. Given that the time at the counter is an average of 10 minutes then some of these lead times seem quite long. Some customers spend more time waiting than being served. And we sense that the performance is getting worse over time.

So for the next experiment we decide to open a sixth counter and to rope off a sixth queue. We expect that increasing capacity will reduce waiting time and we confidently expect the performance to improve.

On day #2 we run our experiment again, letting customers in one every 2 minutes as before and this time we use all the numbers on the dice to decide which queue to direct each customer to. At the end of the hour we collect the slips, calculate the lead times and plot the data – on the same chart.

This is what we see.

It does not look much better and that is big surprise!

The wide variation from customer to customer looks about the same but with the Eye of Optimism we get a sense that the overall performance looks a bit more stable.

So we conclude that adding capacity (and cost) may make a small difference.

But then we remember that we still only served 30 customers – which means that our income stayed the same while our cost increased by 20%. That is definitely NOT good for business: it is not goiug to look good in a business case “possible marginally better quality and 20% increase in cost and therefore price!”

So on day #3 we change the layout. This time we go back to five counters but we re-arrange the ropes to create a single-queue so the customer at the front can be ‘pulled’ to the first available counter. Everything else stays the same – one customer arriving every 2 minutes, the dice, the slips of paper, everything. At the end of the hour we collect the slips, do our sums and plot our chart.

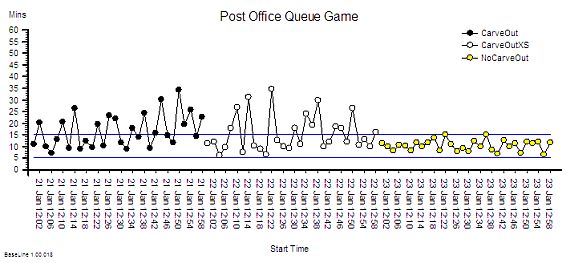And this is what we get! The improvement is dramatic. Both the average and the variation has fallen – especially the variation. But surely this cannot be right. The improvement is too good to be true. We check our data again. Yes, our customers arrived and departed on average one every 2 minutes as before; and all our operatives did the work in an average of 10 minutes just as before. And we had the exactly the same capacity as we had on day #1. And we finished on time. It is correct. We are gobsmaked. It is like a magic wand has been waved over our process. We never would have predicted that just moving the ropes around to could have such a big impact. The Queue Theorists were correct after all!

But wait a minute! We are delivering a much better customer experience in terms of waiting time and at the same cost. So could we do even better with six counters open? What will happen if we keep the single-queue design and open the sixth desk? Before it made little difference but now we doubt our ability to guess what will happen. Our intuition seems to keep tricking us. We are losing our confidence in predicting what the impact will be. We are in counter-intuitive land! We need to run the experiment for real.

So on day #4 we keep the single-queue and we open six desks. We await the data eagerly.

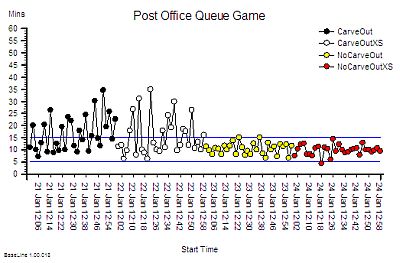And this is what happened. Increasing the capacity by 20% has made virtually no difference – again. So we now have two pieces of evidence that say – adding extra capacity did not make a difference to waiting times. The variation looks a bit less though but it is marginal.

It was changing the Queue Design that made the difference! And that change cost nothing. Rien. Nada. Zippo!

That will look much better in our report but now we have to face the emotional discomfort of having to re-evaluate one of our deepest held assumptions.

Reality is telling us that we are delivering a better quality experience using exactly the same resources and it cost nothing to achieve. Higher quality did NOT cost more. In fact we can see that with a carve-out design when we added capacity we just increased the cost we did NOT improve quality. Wow! That is a shock. Everything we have been led to believe seems to be flawed.

Our senior managers are not going to like this message at all! We will be challening their dogma directly. And they do not like that. Oh dear!

Now we can see how much better a no-carveout single-queue pull-design can work; and now we can explain why single-queue designs are used; and now we can show others our experiment and our data and if they do not believe us they can repeat the experiment themselves. And we can see that it does not need a real Post Office – a pad of Post It® Notes, a few stopwatches and some willing helpers is all we need.

And even though we have seen it with our own eyes we still struggle to explain how the single-queue design works better. What actually happens? And we still have that niggling feeling that the performance on day #1 was unstable. We need to do some more exploring.

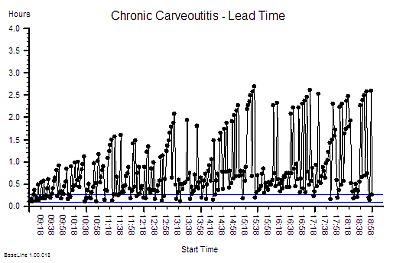
So we run the day#1 experiment again – the five queues – but this time we run it for a whole day, not just an hour.

Ah ha! Our hunch was right. It is an unstable design. Over time the variation gets bigger and bigger.

But how can that happen?

Then we remember. We told the customers that they could not choose the shortest queue or change queue after they had joined it. In effect we said “do not look at the other queues“.

And that happens all the time on our systems when we jealously hide performance data from each other! If we are seen to have a smaller queue we get given extra work by the management or told to slow down by the union rep!

So what do we do now? All we are doing is trying to improve the service and all we seem to be achieving is annoying more and more people.

What if we apply a maximum waiting time target, say of 1 hour, and allow customers to jump to the front of their queue if they are at risk if breaching the target? That will smooth out spikes and give everyone a fair chance. Customers will understand. It is intuitively obvious and common sense. But our intuition has tricked us before …

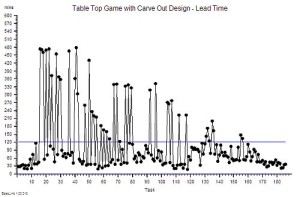
So we run the experiment again and this time we tell our customers that if they wait 50 minutes then they can jump to the front of their queue. They appreciate this because they now have a upper limit on the time they will wait.

And this is what we observe. It looks better than before, at least initially, and then it goes pear-shaped.

All we have done with our ‘carve-out and-expedite-the-long-waiters’ design is to defer the inevitable – the crunch. We cannot keep our promise. By the end everyone is pushing to the frontof the queue. It is a riot!

And there is more. Look at the lead time for the last few customers – two hours. Not only have they waited a long time, but we have had to stay open for two hours longer. That is a BIG cost pessure in overtime payments.

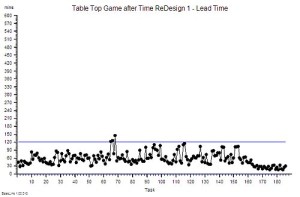
So, whatever way we look at it: a single-queue design is better. And no one loses out! The customers have a short and predictable waiting time; the operatives are kept occupied and go home on time; and the executives bask in the reflected glory of the excellent customer feedback. It is a Three Wins® design.

Seeing is believing – and we now know that it is worth diagnosing and treating carveoutosis.

And the only thing left to do is to explain is how a single-queue design works better. It is not obvious is it?

And the best way to do that is to play the Post Office Game and see what actually happens.

A big light-bulb moment awaits!

Update: My little Sylvanian friends have tried the Post Office Game and kindly sent me this video of the before Sylvanian Post Office Before and the after Sylvanian Post Office After. They say they now know how the single-queue design works better.

19/01/2013

A Ray Of Hope

It does not seem to take much to bring a real system to an almost standstill. Six inches of snow falling between 10 AM and 2 PM in a Friday in January seems to be enough!

It was not so much the amount of snow – it was the timing. The decision to close many schools was not made until after the pupils had arrived – and it created a logistical nightmare for parents.

Many people suddenly needed to get home before they expected which created an early rush hour and gridlocked the road system.

The same number of people travelled the same distance in the same way as they would normally – it just took them a lot longer. And the queues created more problems as people tried to find work-arounds to bypass the traffic jams.

How many thousands of hours of life-time was wasted sitting in near-stationary queues of cars? How many millions of poundsworth of productivity was lost? How much will the catchup cost?

And yet while we grumble we shrug our shoulders and say “It is just one of those things. We cannot control the weather. We just have to grin and bear it.”

Actually we do not have to. And we do not need a weather machine to control the weather. Mother Nature is what it is.

Exactly the same behaviour happens in many systems – and our conclusion is the same. We assume the chaos and queues are inevitable.

They are not.

They are symptoms of the system design – and specifically they are the inevitable outcomes of the time-design.

But it is tricky to visualise the time-design of a system. We can see the manifestations of the poor time-design, the queues and chaos, but we do not so easily perceive the causes. So the poor time-design persists. We are not completely useless though; there are lots of obvious things we can do. We can devise ingenious ways to manage the queues; we can build warehouses to hold the queues; we can track the jobs in the queues using sophisticated and expensive information technology; we can identify the hot spots; we can recruit and deploy expediters, problem-solvers and fire-fighters to facilitate the flow through the hottest of them; and we can pump capacity and money into defences, drains and dramatics. And our efforts seem to work so we congratulate ourselves and conclude that these actions are the only ones that work. And we keep clamouring for more and more resources. More capacity, MORE capacity, MORE CAPACITY.

Until we run out of money!

And then we have to stop asking for more. And then we start rationing. And then we start cost-cutting. And then the chaos and queues get worse.

And all the time we are not aware that our initial assumptions were wrong.

The chaos and queues are not inevitable. They are a sign of the time-design of our system. So we do have other options. We can improve the time-design of our system. We do not need to change the safety-design; nor the quality-design; nor the money-design. Just improving the time-design will be enough. For now.

So the $64,000,000 question is “How?”

Before we explore that we need to demonstrate What is possible. How big is the prize?

The class of system design problem that cause particular angst are called mixed-priority mixed-complexity crossed-stream designs. We encounter dozens of them in our daily life and we are not aware of it. One of particular interest to many is called a hospital. The mixed-priority dimension is the need to manage some patients as emergencies, some as urgent and some as routine. The mixed-complexity dimension is that some patients are easy and some are complex. The crossed-stream dimension is the aggregation of specialised resources into departments. Expensive equipment and specific expertise. We then attempt to push patients with different priorites long different paths through these different departments . And it is a management nightmare!

Our usual and “obvious” response to this challenge is called a carve-out design. And that means we chop up our available resource capacity into chunks. And we do that in two ways: chunks of time and chunks of space. We try to simplify the problem by dissecting it into bits that we can understand. We separate the emergency departments from the planned-care facilities. We separate outpatients from inpatients. We separate medicine from surgery – and we then intellectually dissect our patients into organ systems: brains, lungs, hearts, guts, bones, skin, and so on – and we create separate departments for each one. Neurology, Respiratory, Cardiology, Gastroenterology, Orthopaedics, Dermatology to list just a few. And then we become locked into the carve-out design silos like prisoners in cages of our own making.

And so it is within the departments that are sub-systems of the bigger system. Simplification, dissection and separation. Ad absurdam.

The major drawback with our carve-up design strategy is that it actually makes the system more complicated. The number of necessary links between the separate parts grows exponentially. And each link can hold a small queue of waiting tasks – just as each side road can hold a queue of waiting cars. The collective complexity is incomprehensible. The cumulative queue is enormous. The opportunity for confusion and error grows exponentially. Safety and quality fall and cost rises. Carve-out is an inferior time-design.

But our goal is correct: we do need to simplify the system so that means simplifying the time-design.

To illustrate the potential of this ‘simplify the time-design’ approach we need a real example.

One way to do this is to create a real system with lots of carve-out time-design built into it and then we can observe how it behaves – in reality. A carefully designed Table Top Game is one way to do this – one where the players have defined Roles and by following the Rules they collectively create a real system that we can map, measure and modify. With our Table Top Team trained and ready to go we then pump realistic tasks into our realistic system and measure how long they take in reality to appear out of the other side. And we then use the real data to plot some real time-series charts. Not theoretical general ones – real specific ones. And then we use the actual charts to diagnose the actual causes of the actual queues and actual chaos.

This is the time-series chart of a real Time-Design Game that has been designed using an actual hospital department and real observation data. Which department it was is not of importance because it could have been one of many. Carve-out is everywhere.

During one run of the Game the Team processed 186 tasks and the chart shows how long each task took from arriving to leaving (the game was designed to do the work in seconds when in the real department it took minutes – and this was done so that one working day could be condensed from 8 hours into 8 minutes!)

There was a mix of priority: some tasks were more urgent than others. There was a mix of complexity: some tasks required more steps that others. The paths crossed at separate steps where different people did defined work using different skills and special equipment. There were handoffs between all of the steps on all of the streams. There were lots of links. There were many queues. There were ample opportunities for confusion and errors.

But the design of the real process was such that the work was delivered to a high quality – there were very few output errors. The yield was very high. The design was effective. The resources required to achieve this quality were represented by the hours of people-time availability – the capacity. The cost. And the work was stressful, chaotic, pressured, and important – so it got done. Everyone was busy. Everyone pulled together. They helped each other out. They were not idle. They were a good team. The design was efficient.

The thin blue line on the time-series chart is the “time target” set by the Organisation. But the effective and efficient system design only achieved it 77% of the time. So the “obvious” solution was to clamour for more people and for more space and for more equipment so that the work can be done more quickly to deliver more jobs on-time. Unfortunately the Rules of the Time-Design Game do not allow this more-money option. There is no more money.

To succeed at the Time-Design Game the team must find a way to improve their delivery time performance with the capacity they have and also to deliver the same quality. But this is impossible! If it were possible then the solution would be obvious and they would be doing it already. No one can succeed on the Time-Design Game.

Wrong. It is possible. And the assumption that the solution is obvious is incorrect. The solution is not obvious – at least to the untrained eye.

To the trained eye the time-series chart shows the characteristic signals of a carve-out time-design. The high task-to-task variation is highly suggestive as is the pattern of some of the earlier arrivals having a longer lead time. An experienced system designer can diagnose a carve-out time-design from a set of time-series charts of a process just as a doctor can diagnose the disease from the vital signs chart for a patient. And when the diagnosis is confirmed with a verification test then the time-Redesign phase can start.

This chart shows what happened after the time-design of the system was changed – after some of the carve-out design was modified. The Y-axis scale is the same as before – and the delivery time improvement is dramatic. The Time-ReDesigned system is now delivering 98% achievement of the “on time target”.

The important thing to be aware of is that exactly the same work was done, using exactly the same steps, and exactly the same resources. No one had to be retrained, released or recruited. The quality was not impaired. And the cost was actually less because less overtime was needed to mop up the spillover of work at the end of the day.

And the Time-ReDesigned system feels better to work in. It is not chaotic; flow is much smoother; and it is busy yet relaxed and even fun. The same activity is achieved by the same people doing the same work in the same sequence. Only the Time-Design has changed. A change that delivered a win for the workers!

What was the impact of this cost-saving improvement on the customers of this service? They can now be 98% confident that they will get their task completed correctly in less than 120 minutes. Before the Time-Redesign the 98% confidence limit was 470 minutes! So this is a win for the customers too!

And the Time-ReDesigned system is less expensive so it is a win for whoever is paying.

Same safety and quality, quicker with less variation, and at lower cost. Win-Win-Win.

And the usual reaction to playing the Time-ReDesign Game is incredulous disbelief. Some describe it as a “light bulb” moment when they see how the diagnosis of the carve-out time-design is made and and how the Time-ReDesign is done. They say “If I had not seen it with my own eyes I would not have believed it.” And they say “The solutions are simple but not obvious!” And they say “I wish I had learned this years ago!” And thay apologise for being so skeptical before.

And there are those who are too complacent, too careful or too cynical to play the Time-ReDesign Game (which is about 80% of people actually) – and who deny themselves the opportunity of a win-win-win outcome. And that is their choice. They can continue to grin and bear it – for a while longer.

And for the 20% who want to learn how to do Time ReDesign for real in their actual systems there is now a Ray Of Hope.

And the Ray of Hope is illuminating a signpost on which is written “This Way to Improvementology“.

12/01/2013

Quality First or Time First?

Before we explore this question we need to establish something. If the issue is Safety then that always goes First – and by safety we mean “a risk of harm that everyone agrees is unacceptable”.

Many Improvement Zealots state dogmatically that the only way reach the Nirvanah of “Right Thing – On Time – On Budget” is to focus on Quality First.

This is incorrect. And what makes it incorrect is the word only.

Experience teaches us that it is impossible to divert people to focus on quality when everyone is too busy just keeping afloat. If they stop to do something else then they will drown. And they know it.

The critical word here is busy.

‘Busy’ means that everyone is spending all their time doing stuff – important stuff – the work, the checking, the correcting, the expediting, the problem solving, and the fire-fighting. They are all busy all of the time.

So when a Quality Zealot breezes in and proclaims ‘You should always focus on quality first … that will solve all the problems’ then the reaction they get is predictable. The weary workers listen with their arms-crossed, roll-their eyes, exchange knowing glances, sigh, shrug, shake their heads, grit their teeth, and trudge back to fire-fighting. Their scepticism and cynicism has been cut a notch deeper. And the weary workers get labelled as ‘Not Interested In Quality’ and ‘Resisting Change’ and ‘Laggards’ by the Quality Zealot who has spent more time studying and regurgitating rhetoric than investing time in observing and understanding reality.

The problem here is the seemingly innocuous word ‘always’. It is too absolute. Too black-and-white. Too dogmatic. Too simple.

Sometimes focussing on Quality First is a wise decision. And that situation is when there is low-quality and idle-time. There is some spare capacity to re-invest in understanding the root causes of the quality issues, in designing them out of the process, and in implementing the design changes.

But when everyone is busy – when there is no idle-time – then focussing on quality first is not a wise decision because it can actually make the problem worse!

[The Quality Zealots will now be turning a strange red colour, steam will be erupting from their ears and sparks will be coming from their finger-tips as they reach for their keyboards to silence the heretical anti-quality lunatic. “Burn, burn, burn” they rant].

When everyone is busy then the first thing to focus on is Time.

And because everyone is busy then the person doing the Focus-on-Time stuff must be someone else. Someone like an Improvementologist. The Quality Zealot is a liability at this stage – but they become an asset later when the chaos has calmed.

And what our Improvementologist is looking for are queues – also known as Work-in-Progress or WIP.

Why WIP? Why not where the work is happening? Why not focus on resource utilisation? Isn’t that a time metric?

Yes, resource utilisation is a time-related metric but because everyone is busy then resource utilisation will be high. So looking at utilisation will only confirm what we already know. And everyone is busy doing important stuff – they are not stupid – they are busy and they are doing their best given the constraints of their process design.

The queue is where an Improvementologist will direct attention first. And the specific focus of their attention is the cause of the queue.

This is because there is only one cause of a queue: a mismatch-over-time between demand and activity.

So, the critical first step to diagnosing the cause of a queue is to make the flow visible – to plot the time-series charts of demand, activity and WIP. Until that is done then no progress will be made with understanding what is happening and it wil be impossible to decide what to do. We need a diagnosis before we can treat. And to get a diagnosis we need data from an examination of our process; and we need data on the history of how it has developed. And we need to know how to convert that data into information, and then into understanding, and then into design options, and then into a wise decision, and then into action, and then into improvement.

And we now know how to spot an experienced Improvementologist because the first thing they will look for are the Queues not the Quality.

But why bother with the flow and the queues at all? Customers are not interested in them! If time is the focus then surely it is turnaround times and waiting times that we need to measure! Then we can compare our performance with our ‘target’ and if it is out of range we can then apply the necessary ‘pressure’!

This is indeed what we observe. So let us explore the pros and cons of this approach with an example.

We are the manager of a support department that receives requests, processes them and delivers the output back to the sender. We could be one of many support departments in an organisation: human resources, procurement, supplies, finance, IT, estates and so on. We are the Backroom Brigade. We are the unsung heros and heroines.

The requests for our service come in different flavours – some are easy to deal with, others are more complex. They also come with different priorities – urgent, soon and routine. And they arrive as a mixture of dribbles and deluges. Our job is to deliver high quality work (i.e. no errors) within the delivery time expected by the originator of the request (i.e. on time). If we do that then we do not get complaints (but we do not get compliments either).

From the outside things look mostly OK. We deliver mostly on quality and mostly on time. But on the inside our department is in chaos! Every day brings a new fire to fight. Everyone is busy and the pressure and chaos are relentless. We are keeping our head above water – but only just. We do not enjoy our work-life. It is not fun. Our people are miserable too. Some leave – others complain – others just come to work, do stuff, take the money and go home – like Zombies. They comply.

Once in the past we were were seduced by the sweet talk of a Quality Zealot. We were promised Nirvanah. We were advised to look at the quality of the requests that we get. And this suggestion resonated with us because we were very aware that the requests were of variable quality. Our people had to spend time checking-and-correcting them before we could process them. The extra checking had improved the quality of what we deliver – but it had increased our costs too. So the Quality Zealot told us we should work more closely with our customers and to ‘swim upstream’ to prevent the quality problems getting to us in the first place. So we sent some of our most experienced and most expensive Inspectors to paddle upstream. But our customers were also very busy and, much as they would have liked, they did not have time to focus on quality either. So our Inspectors started doing the checking-and-correcting for our customers. Our people are now working for our customers but we still pay their wages. And we do not have enough Inspectors to check-and-correct all the requests at source so we still need to keep a skeleton crew of Inspectors in the department. And these stay-at-home Inspectors are stretched too thin and their job is too pressured and too stressful. So no one wants to do it.And given the choice they would all rather paddle out to the customers first thing in the morning to give them as much time as possible to check-and-correct the requests so the days work can be completed on time. It all sounds perfectly logical and rational – but it does not seem to have worked as promised. The stay-at-home Inspectors can only keep up with the more urgent work, delivery of the less urgent work suffers and the chronic chaos and fire-fighting are now aggravated by a stream of interruptions from customers asking when their ‘non-urgent’ requests will be completed.

The Quality Zealot insisted we should always answer the phone to our customers – so we take the calls – we expedite the requests – we solve the problems – and we fight-the-fire. Day, after day, after day.

We now know what Purgatory means. Retirement with a pension or voluntary redundancy with a package are looking more attractive – if only we can keep going long enough.

And the last thing we need is more external inspection, more targets, and more expensive Quality Zealots telling us what to do!

And when we go and look we see a workplace that appears just as chaotic and stressful and angry as we feel. There are heaps of work in progress everywhere – the phone is always ringing – and our people are running around like headless chickens, expediting, fire-fighting and getting burned-out: physically and emotionally. And we feel powerless to stop it. So we hide.

Does this fictional fiasco feel familiar? It is called the Miserable Job Purgatory Vortex.

Now we know the characteristic pattern of symptoms and signs: constant pressure of work, ever present threat of quality failure, everyone busy, just managing to cope, target-stick-and-carrot management, a miserable job, and demotivated people.

The issue here is that the queues are causing some of the low quality. It is not always low quality that causes all of the queues.

Queues create delays, which generate interruptions, which force investigation, which generates expediting, which takes time from doing the work, which consumes required capacity, which reduces activity, which increases the demand-activity mismatch, which increases the queue, which increases the delay – and so on. It is a vicious circle. And interruptions are a fertile source of internally generated errors which generates even more checking and correcting which uses up even more required capacity which makes the queues grow even faster and longer. Round and round. The cries for ‘we need more capacity’ get louder. It is all hands to the pump – but even then eventually there is a crisis. A big mistake happens. Then Senior Management get named-blamed-and shamed, money magically appears and is thrown at the problem, capacity increases, the symptoms settle, the cries for more capacity go quiet – but productivity has dropped another notch. Eventually the financial crunch arrives.

One symptom of this ‘reactive fire-fight design’ is that people get used to working late to catch up at the end of the day so that the next day they can start the whole rollercoaster ride again. And again. And again. At least that is a form of stability. We can expect tomorrow to be just a s miserable as today and yesterday and the day before that. But TOIL (Time Off In Lieu) costs money.

The way out of the Miserable Job Purgatory Vortex is to diagnose what is causing the queue – and to treat that first.

And that means focussing on Time first – and that means Focussing on Flow first. And by doing that we will improve delivery, improve quality and improve cost because chaotic systems generate errors which need checking and correcting which costs more. Time first is a win-win-win strategy too.

And we already have everything we need to start. We can easily count what comes in and when and what goes out and when.

The first step is to plot the inflow over time (the demand), the outflow over time (the activity), and from that we work out and plot the Work-in-Progress over time. With these three charts we can start the diagnostic process and by that path we can calm the chaos.

And then we can set to work on the Quality Improvement.

13/01/2013 – Newspapers report that 17 hospitals are “dangerously understaffed” Sound familiar?

Next week we will explore how to diagnose the root cause of a queue using Time charts.

For an example to explore please play the SystemFlow Game by clicking here

05/01/2013

The Management of Victimosis

One of the commonest psycho-socio-economic diseases is Victimosis.

This disease has a characteristic set of symptoms and signs. The symptoms are easy to detect – and the easiest way is to close your eyes and listen to the language being used. There is a characteristic vocabulary. ‘Yes but’ is common as is ‘If only’ and ‘They should’ and ‘Not my’ and ‘Too busy’. Hearing these phrases used frequently is good evidence that the subject is suffering from Victimosis.

Everyone suffers from Acute Victimosis occasionally, especially if they are tired and suffer a series of emotional set backs. With the support of relatives and friends our psychoimmune system is able to combat the cause and return us to healthy normality. We are normally able to heal our emotional wounds.

Unfortunately Victimosis is an infectious and highly contagious condition and with a large enough innoculum it can spread until almost everyone in the organisation is affected to some degree. When this happens the Victimosis behaviour can become the norm and awareness of the symptoms slips from consciousness. Victimosis then becomes the unspoken dominant culture and the transition to the Chronic Victimosis phase is complete.

Research has shown that Victimosis is an acquired disease linked to a transmissable meme that is picked up early in life. The meme can be transmitted person-to-person and also through mass communication systems which then leads to rapid dissemination. Typical channels are newspapers, television, the internet and now social media. Just sample the daily news and observe how much Victimosis language is in circulation.

Those more susceptible to infection can develop into chronic carriers who constantly infect and reinfect others. The outward mainfestations of the chronic form are incessant complaining, criticising, irrational decisions, ineffective actions, blaming and eventually depression, hopelessness and terminal despair. The chronically infected may aggregate into like-minded groups as a safety-in-numbers reflex response. These groups are characterised by having a high proportion of people with the same temperament; particularly the Guardian preference (the Supervisors, Inspectors, Providers and Protectors who make up two thirds of the population).

Those able to resist infection find the context and culture toxic and they take action. They leave.

The outward manifestations of Chronic Victimosis are GroupThink and Silosis. GroupThink is where collectives start to behave as one and their group-rhetoric becomes progressively less varied and more dogmatic. Silosis is a form of organisational tribalism where Departments become separated from each other, conceptually, emotionally, physically and financially. Both natural reactions only aggravate the condition and accelerate the decline.

One of the effects of the Victimosis-meme is Agnostic Hyper-Reactivity. This is where both the Individuals and their Silos develop a thick emotional protective membrane that distorts their perception. It is not that they do not sense what is happening – it is that they do not perceive it or that they perceive it in a distorted way. This is the Agnosia part – literally ‘not knowing’.

Unfortunately being ignorant of Reality does not help and eventually the pressure of Reality builds up and punches a hole through the emotional barrier. Something exceptionally bad happens that cannot be discounted or ignored. This is the ‘crisis‘ stage and it elicits a characteristic reflex reaction. An emotional knee-jerk. Unfortunately the reflex is an over-reaction and is poorly focussed and badly coordinated – so it does more harm than good.

This is the hyper-reactivity part.

The blind reflex reaction further destabilises an already unstable situation and accelerates the decline. It creates a positive feedback loop that can quickly escalate to verbal, written and then psychological and physical conflict. The Lose-Lose-Lose of Self-Destructive behaviour that is characteristic of the late phase. And that is not all. Over time the reflex reaction gets less effective as the Victimosis Membrane thickens. The reflex fades out. This is a dangerous development because on the surface it looks like things are improving, there is less conflict, but in reality the patient is slipping into pre-terminal Victimosis.

Fortunately there is a treatment for Victimosis.

It is called Positivicillin.

This is not a new wonder drug, it is a natural product. We all produce Positivicillin and some of us produce more than others: they are called Optimists. Positivicillin works by channelling the flow of emotional energy into the reflection-and-action pathways. Naturally occurring Positivicillin has a long-half life: the warm glow of success lasts a long time. Unfortunately Positivicillin is irreversibly deactivated by the emotional toxin generated by the Victimosis meme: a toxin called Discountin. So in the presence of Discountin the affected person needs to generate more Positivicillin and to do so continuously and this leads to emotional exhaustion. The diffusion of Positivicillin is impeded by the Victimosis Membrane so if subject has a severe case of Chronic Victimosis then they may need extrinsic Positivicillin treatment at high dose and for a long time to prevent terminal decline. The primary goal of emergency treatment is to neutralise the excess Discountin for long enough that the natural production of Positivicillin can start to work.

So where can we get supplies of extrinsic Positivicillin from?

In its pure form Positivicillin is rare and expensive. The number of naturally occurring Eternal Optimist Exporters is small and their collective Positivicillin production capability is limited. Healthy organisations value and attract them; unhealthy ones discount and reject them.

So we are forced to resort to using more abundant, cheaper but inferior drugs. One is called Alcoholimycin and another is Tobaccomycin. They are both widely available and affordable but they have long term irreversible toxic side effects.

Chronic Victimosis is endemic so chronic abuse of Tobaccomycin and Alcoholimycin is common and, in an attempt to restrict their negative long term effects, both drugs are heavily taxed by the Authorities.

Unfortunately this only aggravates the spread of Chronic Victimosis which some report is a sign of the same condition affecting the Authorties! These radicals are calling for de-regulation of the more potent variants such a Cannabisimycin but the Authorities have opted for a tightly regulated supply of symptom-suppressants such as Anxiolytin and Antidepressin. These are now freely available and do help those who want to learn to cure themselves.

The long term goal of the Victimosis Research Council is to develop ways to produce pure Positivicillin and to treat the most severe cases of Chronic Victimosis; and to find ways to boost the natural production of Positivicillin within less seriously affected individuals and organisations.

Chronic Victimosis is not a new disease – it has been described in various forms throughout recorded history – so the search for a cure starts with the historical treatments – one of which is Confessmycin. This has been used for centuries and appears to work well for some but not others and this idiosyncratic response is believed to be due to the presence (or not) of the Rel-1-Gion meme. Active dissemination of a range of Rel-1-Gion meme variants (and the closely linked Pol-1-Tic meme variants) has been tried with considerable success but does not appear to be a viable long term option.

A recent high-tech approach is called a Twimplant. This is an example of the Social-Media class of biopsychosocial feedback loops that uses the now ubiquitous mobiphonic symbiont to connect the individual to a regular supply of positive support, ideas and evidence called P-Tweets. It is important to tune the Twimplant correctly because the same device can also pick up distress signals broadcast by sufferers of Chronic Victimosis who are attempting to dilute their Discountin by digitising it and exporting it to everyone else. These are called N-Tweets and are easily identifiable by their Victimosis vocabulary. N-tweets can be avoided by adopting an Unfollow policy.

One promising line of new research is called R2LM probe therapy. This is an unconventional and innovative way of curing Chronic Victimosis. The R2LM probe is designed to identify the gaps in the organisational memetic code and to guide delivery of specific meme transplants that fill the gaps it reveals. One common gap is called the OM-meme deletion and one effective treatment for this is called FISH. Taking a course of FISH injections or using a FISH immersion technique leads to a rapid and sustained improvement in emotional balance. That in-turn leads to an increase in the natural production of Positivicillin. From that point on the individual and can dissolve the Victimosis Membrance and correct their perceptual distortion. The treatment is sometimes uncomfortable but those who completed the course will vouch for its effectiveness.

For the milder forms of Victimosis it is possible to self-diagnose and to self-treat.

The strategy here is to actively reduce the production of Discountin and to boost the natural production of Positivicillin. These have a synergistic effect. The first step is to practice listening for the Victimosis vocabulary using a list of common phrases. The patient is taught to listen for these in spoken communication and to look for them in written communication. Spoken communication includes their Internal Voice. The commonest phrases are:

1. “Yes but …”
2. “If only …”
3. “I/You/We/They should …”
4. “I/We can’t …”
5. “I/We hope …”
6. “Not My/Our fault …”
7. “Constant struggle …”
8. “I/We do not know …”
9. “I am too busy to …”

The negative emotional impact of these phrases is caused by the presence of the Discountin toxin.

The second step is to substitute the contaminated phrase with an equivalent one where the Discountin is deactivated using Positivicillin. This deliberate and conscious substitution is easiest in written communication, then externally spoken and finally the Internal Voice. The replacements for the above are …

1. “Yes, and …”
2. “Next time …”
3. “I/We could …”
4. “I/We can …”
5. “I/We know …”
6. “My/Our responsibility …”
7. “Endless opportunity …”
8. “I/We will learn …”
9. “It is too important not to …”

The system-wide benefits of the prompt and effective management of Chronic Victimosis are enormous. There is more reflective consideration and more effective action. There is success and celebration where before there was failure and frustration. The success stimulates natural release of more Positivicillin which builds a positive reinforcement feedback loop. In addition the other GA-memes become progressively switched off and the signs of Passive Persecutitis and Reactive Rescuopathy resolve.

The combined effect leads to the release of Curiositonin, the natural inquisitiveness hormone, and Excitaline – the hormone that causes the addictive feeling of eager anticipation. The racing heart and the dry mouth.

From then on the ex-patient is able to maintain their emotional balance, to further develop their emotional resilience, and to assist other sufferers. And that is a win for everyone.